筑绘通是一个以 SaaS 形态呈现的复杂的工业软件，在其诸多协作模块中，不同的部分需要应用到不同领域的知识和方法论。其中，如何处理建筑领域中的空间、实体概念，并构建他们之间的复杂关系，是一个基础性的问题。我们运用了多种复合方法来解决问题。除了引入基于计算机视觉、运筹学、拓扑学的工具之外，经典的计算几何工具也发挥很大的作用。并且，在部分问题上，计算几何学方法具有更高的执行效率和求解稳定性。本文旨在介绍经典计算几何学中的一些模型与算法，并探讨其在AI自动出图领域中的潜在作用。
计算几何学
计算几何学是几何学的一个分支，该学科兴起自上世纪七十年代末，主要研究几何问题的计算机表示、分析、修改和综合。计算几何学在美国常常被称为 Computer Aided Geometric Design (CAGD)。1972 年在美国举行的 CAGD 第一次国际会议，标志着计算几何学科的形成。读者可能注意到，CAGD 与建筑领域常用的 CAD 软件仅有一字之差，这也显示了这两个领域的渊源。事实上，计算机辅助设计是计算几何学科诞生以来应用的首个领域。
从几何到计算几何
计算几何作为一个新兴学科，相比于历史悠久的几何学其他分支有什么不同呢？事实上，二者关注的问题类型通常没有本质的差别。例如在计算机辅助设计领域，我们需要计算大量线段之间的交点。在高中数学的解析几何中，计算线段之间的交点也是常见的问题。不过在计算几何中，我们会更加关注问题的规模与求解效率， 这在其他几何学分支中是相对次要的问题。 设想一下，如何以尽可能快的速度计算 最坏的情况下，线段两两相交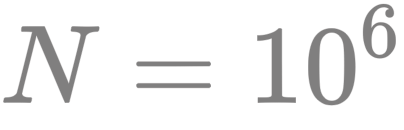 
根线段之间的交点呢？从解析几何的角度来看，直接两两计算交点看起来是非常直接的。不过，这种直截了当的算法需要
的时间，这意味着
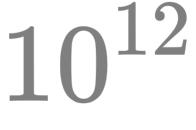数量级的计算。这个数字相对于现代 CPU 的 GHz 主频数量级来说仍然显得十分庞大。当然，如果在最坏的情况，这些线段彼此相交，无论我们采用什么算法，都无可能降低算法时间的数量级。然而，在实际问题中，这种最坏的情况是较少出现的。一般情况下， 线段交点相对于
数量级来说是非常稀疏的，这对于我们涉及更高效的算法提供了改造空间。
在找出所有交点的过程中，如何才能避免对所有的线段对进行测试呢？这里必须利用这种情况的几何特性⎯⎯只有那些相互靠近的线段，才可能会相交；而相距甚远的线段则不可能相交。平面扫描法 (Plane sweep algorithm) 就是基于这一假设设计的。
在算法设计中，找到关键的假设信息，并利用这些假设缩小问题的边界是算法设计的核心。在越是面向现实问题的算法设计中越是重要。
记二维平面上所有待求相交的线段的集合是
。我们将这些线段投影到 y 轴上，将投影定义为它的 y-区间。显然，如果两条直线的 y 区间没有重叠，那么它们一定不会相交。那么，我们只需要在 y 区间重叠的线段之间进行相交测试。
通过投影来排除不可能相交的线段对
完整的平面扫描法有更加复杂流程设计，不过上面的例子足以阐明计算几何的一个特征：即在计算几何算法设计中，我们通常更加关心算法的复杂度与时间空间开销。好在经过长时间的行业积累，大量计算几何问题都有了比较充分的研究和高效的算法实现。
计算几何在建筑自动出图中的应用
「Polygon Decomposition」
在前文《多边形语义分割与图纸中的拓扑特征认知》一文中，我们讨论了多边形分割在建筑自动出图中的重要应用。多边形分割是一个较为复杂的问题，针对分割目标不同，输入条件的不同，可以划分出多种不同的问题场景。在计算几何领域，存在一些较为经典的分割方法。
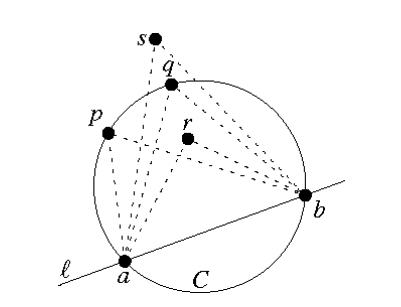
将多边形分割成三角形是最为简单直接的分割方法，学术界和工业界在这一领域的研究较为充分。Delaunay 三角剖分是一种应用十分广泛的三角形剖分方法。严格来说 Delaunay 三角剖分不是一种算法，而是评估一种三角分割是否是一个好的分割的定义，其核心思想是空圆特性和最大化最小角。这两个特性避免了过于狭长的三角形的产生。所谓空圆特性，是指对于任意两个共边的三角形，其中任意一个三角形的完结圆都不能包含另一个三角形的顶点，基于这个原则生成的三角剖分能够实现最小角最大的目标。这一原则成立的原理在于 Thales 定理：
设 C 为一个圆，直线 l 与 C 相交于点 a 和点 b ；另外，在 l 的同一侧有四个点 p,q,r,s，假设 p 和 q 位于圆上，而 r 和 s 分别位于圆内外，则必有
在筑绘通中，我们尝试使用三角剖分进行了连线问题场景中的路由空间剖分，从而实现将路由空间离散化。并在此基础上应用基于图的路由算法。这种方法能够使得路由图的大小与空间尺度无关，而只与空间形态复杂度和障碍物复杂度有关。因此可以显著降低搜索空间，大大提高算法收敛速度（约 3 个数量级），并降低资源占用。
Voroni 分割也是一种多边形分割方法，其定义在一个给定的平面内，按照距离一组给顶点的距离大小将平面分成多个多边形，在每个多边形内部存在一个给定顶点，且多边形内任意一点距离此顶点的距离要小于到其他给定顶点的距离。Voroni 分割在几何、晶体学、建筑学、地理学、气象学、信息系统等许多领域有广泛的应用。python 开源库 centerline 基于 Voroni 分割，实现了寻找“线形”多边形中心线的算法。这些线形多边形可以是道路、桥梁、墙体等结构。
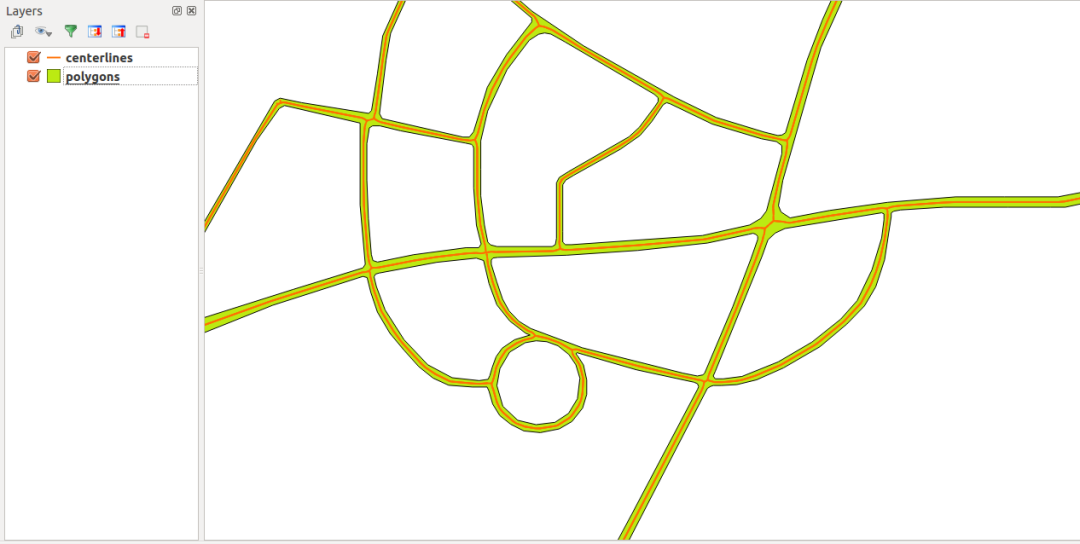
正如我们在上一个章节中提到的，在算法设计中，找到关键的假设信息，并利用这些假设缩小问题的边界是算法设计的核心。需要注意的是，我们并非对任意多边形进行分割，而是在建筑空间领域中针对具有实际含义的墙体、空间轮廓进行分割，这些轮廓多边形具有强烈的整齐性、正交性特征。
「Straight Skeleton」
在几何学中，Straight Skeleton 是一种通过拓扑骨架表示多边形的方法。它在某些方面与中轴相似，但不同之处在于骨架由直线段组成（Straight 含义在此），而多边形的中轴可能包含抛物线。Aichholzer等人首先为简单多边形定义了直骨架，然后由Aichholzer和Aurenhammer推广到平面直线图。Straight Skeleton 可以被理解成多边形的边界线以相同速度向内部的推进时，边之间的交点经过的轨迹。因此不难看出，Straight Skeleton 问题与 Polygon Offsetting 问题在实质上是同一问题。从图面来看，Straight Skeleton 可以被理解成从等高线图中得到的山脊/山谷棱线。
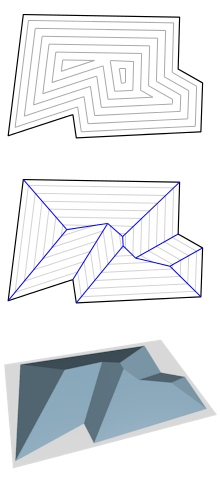
Straight Skeleton 可以将多边形表达为线型元素，可以用来提取多边形的拓扑与结构特征。在筑绘通中，我们广泛使用 Straight Skeleton 进行多边形拆分，多边形形态分析以及性质判定。Straight Skeleton 同样可以用于提取线型多边形中线，相比于 Voroni 方法，Straight Skeleton 方法具有更高的计算效率和稳定性。
「Arrangement and Visibility」
Arrangments 是对 Geometry Arrangements 的简称，中文可以称之为“排列”，其定义为一组几何元素对平面的一个分割。从几何学角度，此处所称的平面可以是指高维平面，而作为分割要素的几何元素亦可以是任意元素：点、直线、曲线、平面、超平面。在 CAD 图纸空间中，我们不难发现，将 CAD 图元作为分割几何元素，则 CAD 图元就构成了二维平面中的一个排列。
考虑一个由线（直线、曲线）在二维平面构成的排列，排列中除分割元素外 ，还包含了这些元素交叉构成的顶点和围合形成的面。
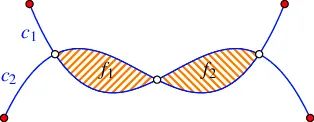
图中给出了平面中的两个曲线 c1 和 c2，这两个曲线产生了两个有界的面 (Faces) f1 和 f2（图中阴影区域）。同时，图中两个曲线还产生了 7 个顶点（包含曲线自身的首尾点）以及 8 个边。若分割元素都是直线，则由下面的定理：
设 L 为由平面上 n 条直线构成的任一集合，而 A(L) 为由 L 导出的排列，则
- A(L) 中的顶点不超过
个； - A(L) 中的边不超过
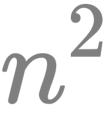条； - A(L) 中的面不超过
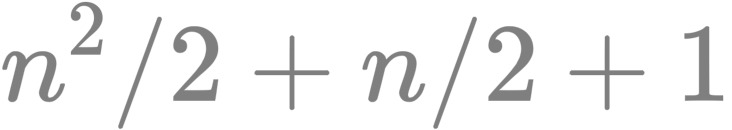张；
除点、边、面以外， 排列中还包含这些要素之间的关系。著名的 C++ 计算几何库 CGAL 使用了一种名为 Half-edge Data Structure 的数据结构来保存排列的关系。在这个数据结构中，每个边被分解成为两个互为孪生的有向向量。每个有向的 halfedge 具有一个 source vertex 和一个 target vertex。Halfedge 用于连接顶点，并分隔面。如果一个顶点 v 是一个 halfedge e 的 target，则称 v 和 e 相邻。对于一个顶点，连接到这个顶点上的边以逆时针的顺序给出。孤立的点没有临边。每个 Halfedge 会存储其相邻的面，这个面位于其左侧。Halfedge 的临边中会有一条边与其具有相同的临面。沿着这个关系从一个边遍历 DCEL 图，最终会回到自身并构成一个闭环，这个闭环被称为一个 connected component of the boundary (CCB)。
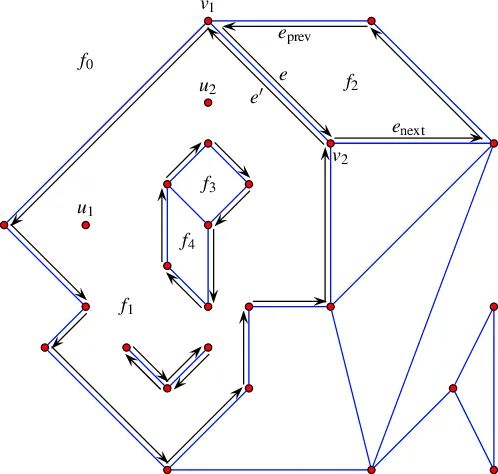
在 CAD 图纸中，若以所有的非标注图元为输入构建排列，则可以基于排列分析得到墙门窗构件要素、空间要素以及他们之间相邻关系，这种关系构成了后续拓扑分析的基础。
「结语」
在本文中我们粗略进行了计算几何的学科介绍，并阐述了集中典型的计算几何模型的基本原理和潜在应用场景。这些理论工具和算法实现是筑绘通 AI 能力的有力援手。未来在我们不断迭代增强筑绘通的各项能力过程中，我们会继续打破各种学科边界，使用更加丰富、立体的技术体系来构建强大的设计大脑。
©版权归品览所有
未经授权请勿转载
RECOMMENDED
一键试用 筑绘通
点击阅读原文或扫码
即刻预约
AlphaDraw筑绘通正逐步上线施工图领域各专业的新模块：包含建筑、结构、暖通、电气、给排水、室内六大专业，47个一级系统，共计180个二级模块。同时，小览也会陆续更新新模块内容及操作教程，敬请期待吧！
品览是AI建筑设计智造者，专注于建筑设计AI服务，致力于为地产企业和设计院客户提供AI设计出图服务。自主研发的建筑AI智能设计云平台AlphaDraw「筑绘通」，基于计算机视觉技术，建筑设计知识库和生成式强化学习算法帮助客户自动完成施工图设计。仅需上传建筑方案图纸就可以自动完善成套施工图，并符合各地设计规范，助力企业标准化出图、效率质量双提升。
本篇文章来源于微信公众号: 品览Pinlan
