约束规划 (Constraint Programming) 是一种数学规划方法,这种方法适合于用来求解通常是 NP 难的组合优化问题。组合优化问题在现实应用场景中非常普遍,涉及人工智能,计算科学以及操作搜索等领域。在建筑设计自动化领域,组合优化问题也非常常见,例如楼梯间详图中的梯段布局问题,地库喷淋中的喷头布局问题等等。一般来说,布局类问题大多可以被建模成组合优化问题。
约束规划
不同于其他典型的规划方法,如线性规划,整型规划等,约束规划更加关注约束本身而非目标函数,约束规划问题甚至可以不定义一个目标函数,目标本身可能表现成为一个特定的约束。这意味着约束规划方法更加关注解的可行性(Feasibility),而非最优性(Optimality)。
一个无目标的约束规划问题被称为一个约束满足问题 (Constraint Satisfaction Problem) ,这个问题可以被表达成一个三元组(X,D,C), 其中
● X={x1, x2, …, xn} 为变量集合;
● D={d1, d2, …, dn} 为变量域,即各个变量的取值集合;
● C={c1, c2, …, cn} 为约束集合。
数学上经典的四色问题中,如何使用四种颜色填充一个平面地图的问题就可以被建模成一个约束满足问题,可以使用约束规划方法进行求解。在数据结构与算法课程上会常遇到的八皇后问题也是典型的 CSP 问题。
CSP 问题是一个典型 NP-hard 问题。约束规划是求解 CSP 问题的一个基本框架,而非特指某种具体的方法。在支持约束规划的工具中,我们通常只需要以声明式的形式定义出 X,D,C 三元组,而不需要指定具体的迭代步骤。相比于其他数据规划方法, 例如在往期文章中介绍的适用于楼梯间梯段布置的混合整型线性规划方法(MILP),约束规划方法对于约束本身的线性形式要求更低,约束规划方法可以适用于更加一般化的问题,尤其是那些难以被建模成线性形式的约束或者效用,因此可以让筑绘通能够解决更加复杂的布置问题。
约束规划的一般求解方法
理论上来说,我们可以用穷举的方法来遍历解空间以期找到可行解。但是由于 CSP 问题的 NP-hard 本质,暴力穷举法在问题规模稍稍增长时便会产生难以接受的时间开销。
「Backtracking」
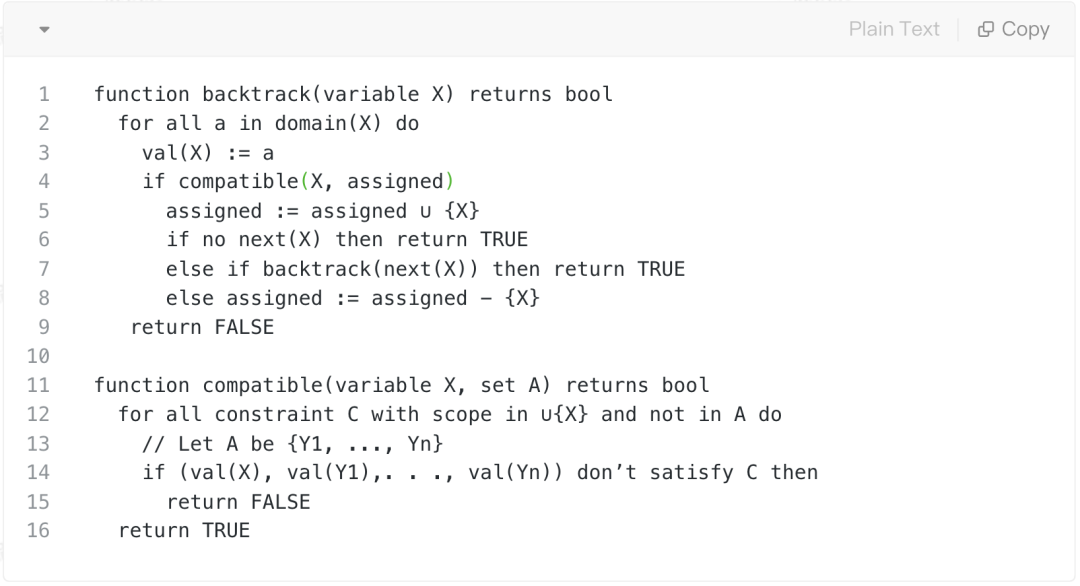
一个更好的思路是 Backtracking,我们可以翻译为回溯法。这个方法的核心思想是维护一个有效的部分解 (partial solution),这里所说的部分解是在该解中只对部分变量进行赋值,而有效部分解则是在强调该部分解符合所有的约束规范。迭代时选取一个部分有效解,并对其进行扩展(即增加一个变量赋值),如果能够扩展到一个有效解,则增加扩展后的有效解到部分有效解集合,否则,我们进行回溯(backtrack),取消(undo)被选取的部分有效解的上一次决策。这一决策过程伪代码如下:
以四皇后问题为例展现这个搜索过程:
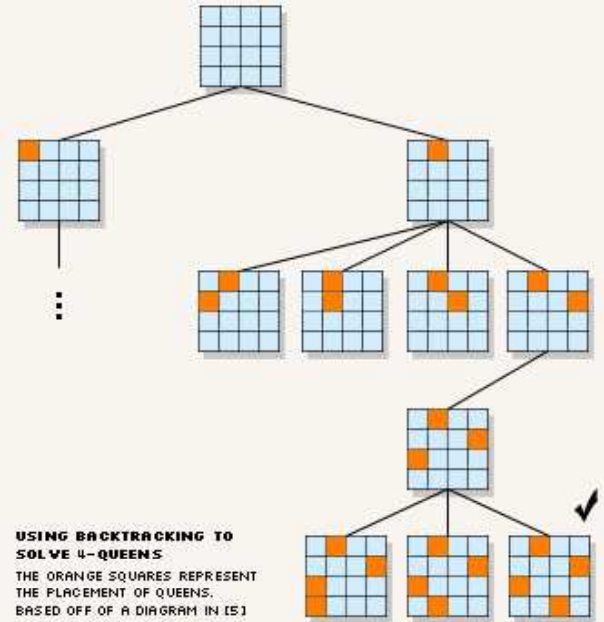
可以看出,Backtracking 方法在解空间的遍历过程是遵循“深度优先”的范式的。在最恶劣的情况下,Backtracking 方法可能也需要遍历整个解空间,但是在实际使用中,Backtracking 方法总是要显著优于暴力穷举法(这一关系类似于快速排序法和冒泡排序法的关系)。
「Propagation」
约束传播法(Constraint Propagation) 的思路也是维护有效的部分解进行树状搜索,不过不同于 Backtracking,约束传播法会将子树中明显不合法的分支删除,从而缩小的搜索空间。由于子树删除存在操作成本,且这一成本与删除子树的范围成正相关。因此如何平衡子树阐述的成本和子树删除的范围成为约束传播法需要考虑的一个核心问题。针对这两个问题的不同设计产生了众多不同类型的约束传播方法。
我们以四皇后问题为例说明约束传播法的子树收敛过程。
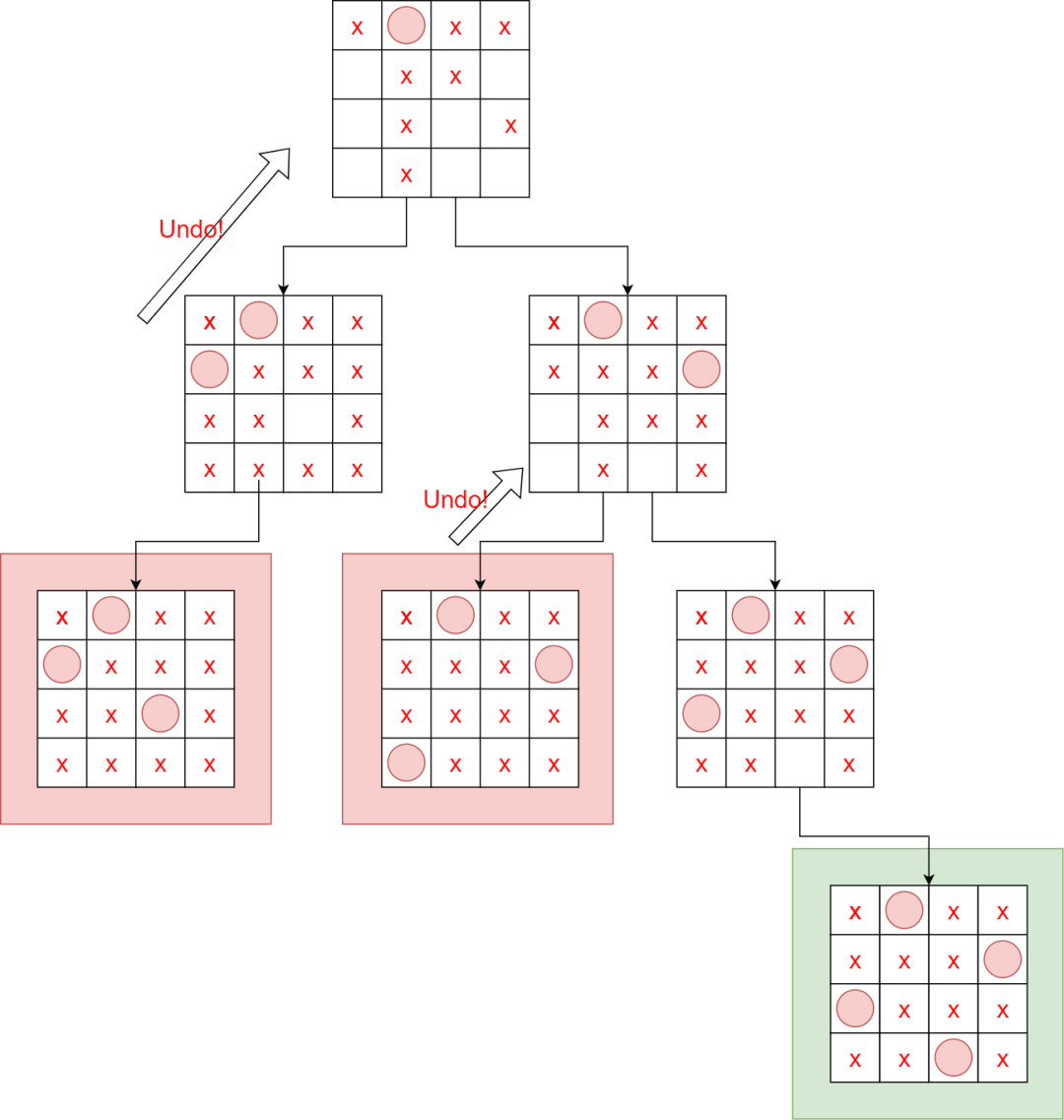
第一步我们将 (0,1)处放上一枚皇后,那么我们可以将其他与该格子处于水平、竖直以及 45 度斜线方向上的其他格子从后续搜索空间中排除。若此时选择左侧分支,可以发现后续步骤无法得到一个完整的有效解,则需要根据 Backtracking 的路径回溯到根节点,并进入右侧分支。在右侧分支,我们在子树中的有效搜索空间内(1,3)处放上第二枚皇后,同样我们可以排除冲突区域,进而缩小解空间,从而以较快的速度收敛到一个可行解。
「小结」
Backtracking 和 Propagation 都是较为基本的算法设计思想,根据细节策略的不同,如初始解的确定方法,确定变量求解顺序,回溯步长及策略,子树删减策略等等的不同,二者都有多种不同的变种,这两种策略也常常混合使用。
通过分析可以发现,Backtracking和Propagation都是一种邻域搜索算法,这种算法都面临“局部最优”的问题,其求解的速度和质量受到初始值(一般可以作为 Hint 提供给变量)的影响较大。在约束的复杂度较高,解空间维度较大时,其收敛速度较慢,在实际使用中我们需要进行针对性的设计。
约束规划在楼梯间详图中的应用
在之前的文章中,我们分享了在楼梯间详图中使用混合整数线性规划方法求解梯段布局问题的方法。随着筑绘通产品的迭代,我们深化了楼梯间详图的设计,将更多的因素纳入到梯段布局问题的考虑中来。例如需要参考建筑模数的要求对休息平台的尺寸取证;又例如需要将梯梁布置纳入考虑,在优化梯段布置的同时优化梯梁的位置。
新增的特性给楼梯间梯段布置的规划模型带来了挑战:
1
新特性进一步扩张了变量的数量,增大了解空间的维度,更重要的是这些新的特性引入了大量的非线性约束,这是混合整数线性规划模型难以处理的;
2
随着楼梯间详图设计的深化,我们增加了用户干预出图形式的多种配置项,这意味着我们需要引入更多的优化目标来引导规划的模型,使其得到具有一定倾向性的解。经典的加权法来处理多目标优化受数值量纲的影响,权重系数调参的结果比较难适应复杂输入条件。如何综合多个优化目标,实现对不同目标优先级的有效控制成为一个核心挑战。
因此,我们约束规划引入了楼梯间梯段布置规划模型,并引入多阶段多目标优化,结合合适的松弛方法,将前序目标设定为后续优化问题的约束项, 从而实现在支持更丰富的约束条件下,实现对多个优化目标的有序优化。
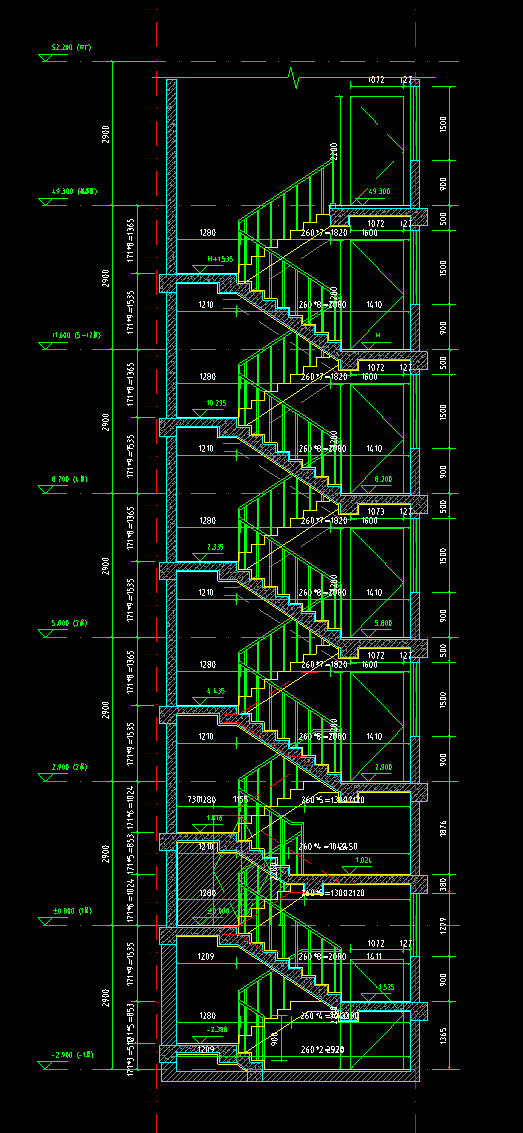
△图例展现了实现碰头控制、平台对齐(左侧平台对齐)台阶数量均衡等多个目标,且符合多种复杂约束的楼梯间梯段布置结果
约束规划在梯段布置中的效果将在新版本中的筑绘通楼梯间详图模块中呈现。
参考文献: [1].https://www.cs.upc.edu/~erodri/webpage/cps/theory/cp/intro/slides.pdf [2].https://en.wikipedia.org/wiki/Constraint_programming [3].https://en.wikipedia.org/wiki/Constraint_satisfaction_problem [4].Computational Mixed-Integer Programming [5].https://developers.google.com/optimization/cp/cp_solver
©版权归品览所有
未经授权请勿转载
RECOMMENDED

一键试用 筑绘通
点击阅读原文或扫码
即刻预约
AlphaDraw筑绘通正逐步上线施工图领域各专业的新模块:包含建筑、结构、暖通、电气、给排水、室内六大专业,47个一级系统,共计180个二级模块。同时,小览也会陆续更新新模块内容及操作教程,敬请期待吧!


品览是AI建筑设计智造者,专注于建筑设计AI服务,致力于为地产企业和设计院客户提供AI设计出图服务。自主研发的建筑AI智能设计云平台AlphaDraw「筑绘通」,基于计算机视觉技术,建筑设计知识库和生成式强化学习算法帮助客户自动完成施工图设计。仅需上传建筑方案图纸就可以自动完善成套施工图,并符合各地设计规范,助力企业标准化出图、效率质量双提升。

-17.png)